Cuando Dios creó el mundo, dispuso 3 torres de diamante. En una de la torres colocó 64 discos de oro con diferentes diámetros. Los discos se encontraban de mayor a menor, situados los de mayor diámetro cerca de la base.
Desde entonces, los monjes de un monasterio cercano mueven los discos uno a uno, con el propósito de que los 64 discos terminen en la tercera torre.
Las reglas para mover los discos son las siguientes:
- No se puede mover más de un disco cada vez.
- No se puede colocar un disco mayor sobre otro menor.
El siguiente programa es un simulador del juego:
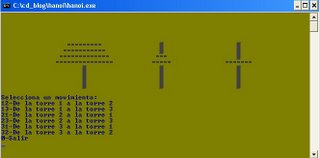
program hanoi;
uses crt;
const
maxDiscos = 64;
type
Tdiscos = array[1..maxDiscos] of integer;
Ttorre = record
numDiscos : integer;
discos : Tdiscos;
end;
var
torre1, torre2, torre3 : Ttorre;
num : integer;
altura: integer;
fin: boolean;
rta: string[2];
i: integer;
numMovimientos: integer = 0;
procedure dibujarEscenario(altura: integer; torre1, torre2, torre3: Ttorre);
var i, j, z: integer;
begin
clrscr;
{Empezamos dibujando las 3 torres sin ning£n disco}
for z:=1 to 3 do
begin
for i:=6 to 13 do
begin
gotoxy(2+z*20, i);
writeln('±');
end;
end;
{Dibujamos los discos de las 3 torres}
{Torre1}
for z:=1 to torre1.numDiscos do
for i:=-torre1.discos[z] to torre1.discos[z] do
begin
gotoxy(22+i,10-z);
writeln('=');
end;
{Torre2}
for z:=1 to torre2.numDiscos do
for i:=-torre2.discos[z] to torre2.discos[z] do
begin
gotoxy(42+i,10-z);
writeln('=');
end;
{Torre3}
for z:=1 to torre3.numDiscos do
for i:=-torre3.discos[z] to torre3.discos[z] do
begin
gotoxy(62+i,10-z);
writeln('=');
end;
end;
procedure moverDisco(var torreOrigen: Ttorre; var torreDestino: Ttorre);
begin
if torreOrigen.numDiscos <> 0 then
if (torreDestino.discos[torreDestino.numDiscos]>
torreOrigen.discos[torreOrigen.numDiscos])
or (torreDestino.numDiscos = 0) then
begin
torreDestino.numDiscos:=torreDestino.numDiscos+1;
torreDestino.discos[torreDestino.numDiscos]:=
torreOrigen.discos[torreOrigen.numDiscos];
torreOrigen.numDiscos:=torreOrigen.numDiscos-1
end
else
begin
gotoxy(1,24);
textcolor(RED);
writeln('MOVIMIENTO NO PERMITIDO');
readln();
textcolor(BLUE);
end
else
begin
gotoxy(1,24);
textcolor(RED);
writeln('LA TORRE SELECCIONADA NO TIENE DISCOS');
readln();
textcolor(BLUE);
end
end;
begin
textcolor(BLUE);
textbackground(YELLOW);
clrscr;
writeln('Torres de Hanoi');
repeat
write('N£mero de discos (entre 1 y 9): ');
readln(num);
until (num>0) and (num<10);
altura:= num;
torre1.numDiscos := num;
for i:=1 to num do
torre1.discos[i]:=num+1-i;
torre2.numDiscos := 0;
torre3.numDiscos := 0;
fin:=false;
repeat
dibujarEscenario(altura, torre1, torre2, torre3);
if torre3.numDiscos = num then
begin
gotoxy(1,24);
textcolor(RED);
writeln('HAS GANADO! N£mero de movimientos realizados: ',
numMovimientos);
writeln('N£mero m¡nimo de movimientos posible: ',
2*num-1);
readln();
fin:=true;
end
else
begin
gotoxy(1,15);
writeln('Selecciona un movimiento:');
writeln('12-De la torre 1 a la torre 2');
writeln('13-De la torre 1 a la torre 3');
writeln('21-De la torre 2 a la torre 1');
writeln('23-De la torre 2 a la torre 3');
writeln('31-De la torre 3 a la torre 1');
writeln('32-De la torre 3 a la torre 2');
writeln('0-Salir');
readln(rta);
if rta = '12' then moverDisco(torre1, torre2);
if rta = '13' then moverDisco(torre1, torre3);
if rta = '21' then moverDisco(torre2, torre1);
if rta = '23' then moverDisco(torre2, torre3);
if rta = '31' then moverDisco(torre3, torre1);
if rta = '32' then moverDisco(torre3, torre2);
if rta = '0' then fin:=true;
numMovimientos:=numMovimientos+1;
end;
until fin;
end.

